群论入门

jokervTv 2021/8/18 群论

模算术
群的定义
子群、陪集、正规子群与商群
循环群
同构
同态
拓扑的同态
Kernel / Image 与零空间/列空间
对称群

“群”的概念被从不同领域中被抽象出来，并演化出环、场、Modules 和向量空间等概念。这些概念，今天统称为抽象代数，也称近世代数 (Morden Algebra)。你要是和一群搞数学的人在一起，他们就称之为“代数”，但你可能发现他们聊的内容的与你印象中的代数完全不同！

# 模算术

抽象代数从多门不同的学问中抽象出相同的概念。在讨论群的定义前，先以模算术 (Modular arithmetic) 为例进行讨论，以便从中进行抽象出群的概念。

模算术：将一组整数分成有限个集合，将这些集合视为一种新的数，这对应于后面我们要讨论的正规子群 (Normal Subgroup) 和商群 (Quotient Group)。

模算术也称时钟算术 (Clock arithmetic)，与日常生活中的时钟逻辑相似，如：11 点后的 4 个小时是 15 点，也就是下午 3 点： $11 + 4 = 15 \equiv 3$ 。符号 $\equiv$ 被首次使用，表示“等于与定义”，读作 “is congruent to”。

因此，采用下图的 0 到 5 标记的时钟，并以此为例进行分析，虽然群的概念尚未正式定义，但不妨碍理解：

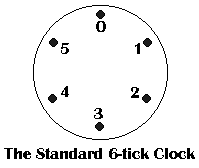
时钟时间只能从集合 (Set) $Z=\left\{0,1,2,3,4,5\right\}$ 中取整数值，不能是 4 点半，集合中包含的对象称为元素 (element) 或成员 (member)，元素排名不分先后；
操作 (Operation): 对时间可以进行 $+$ 操作， $-$ 可表示为 $+$ 一个负数，如： $5-2=5+(-2)$ ；
封闭性 (Closed under operation): 在该时钟上，不论进行任何二元操作 (Binary Operations，如：从集合 $Z$ 中取出两个元素 $2$ 和 $3$ ，进行 $+$ 操作， $2+3=5$ )，结果一定还在集合内（结果取 6 的余数，即 Mod 6)；
恒等元 (Identity): $+0$ 等于什么都不做，原地不动，也可以理解为两个互逆的操作叠加，比如+4 和+2 后回到 0，相等以字母 $e$ 表示；不少文章将 Identity 译为单位元，作为乘法没有问题，作为加法显然就有点不合适了。
逆 (Inverse): 加 4 和减 2 的结果相同， $5+4=9\equiv3=5-2 \quad(mod \space 6)$ ，数学上称 $9$ is "congruent to $3$ mod $6$ ; $4+2=0$ ，因此， $4$ 与 $2$ 互逆。
结合律 (Associativity): $(a+b)+c = a+(b+c)$ .

# 群的定义

例 2：线性子空间，也称向量子空间。

向量子空间 $V$ 具有一下特点：

包含 0 向量，任何向量加 0 向量等于自身 $0+v=v$ ;
加法下封闭
交换律： $v+w=w+v$
逆： $v+(-v)=(-v)+v=0$
结合率： $u+(v+w)=(u+v)+w$

可见：加法下的向量子空间是阿贝尔群。

然而，向量子空间不只是阿贝尔群，向量还可以数乘 $c\in R$ ，这给了向量空间比一般向量空间更多的结构和特点，以后再讨论吧。

我们可以抽象出群的正式定义了：

群 G(Group) 的元素属于一个集合
G 对应的二元操作 (Binary Operation): 以 $\circ$ 表示，此处使用了一个更抽象的符号来代表 $\times$ 和 $+$ ；
封闭性 (Closed under operation): 对 G 的两个元素进行任何操作，结果仍在集合内，即： $x\circ y\in G$ for all $x,y\in G$ ；
恒等元 (Identity): 存在一个元素 $e\in G$ ， $x\circ e=e\circ x=x$ ；
逆 (Inverse): 对每一个 $G$ 的元素 $x$ ，都存在一个元素 $x^{-1}\in G$ ，使得 $x\circ x^{-1}=x^{-1}\circ x=e$ ；
结合律 (Associativity): $(x\circ y)\circ z = x\circ(y\circ z)$ .

群 $G$ 和操作 $\circ$ 写成 $(G,\circ)$ 。

为什么是这 6 条，不能再多一条或少一条吗？这六条正是求解方程所需的最少规则，符合奥卡姆剃刀的要求。

从最简单 Trivial 的只含一个元素 $e$ 的群 ( $|G|=1$ ) 开始，群的元素数量称为群的阶数 (Order of Group)，以 $|G|$ 表示，这个群也称 Trivial Group。

定义 1.1 群：设𝐆是一些元素（操作）的集合，记为𝐆 = {⋯， g， ⋯}，在𝐆中定义了乘运算，如果𝐆中元素对这种运算满足下面四个条件：

封闭性： ∀两个元素（操作）的乘积仍属于这类元素（操作）的集合4；
结合律：对∀三个元素（操作） 𝐟、 𝐠、 𝐡，有(𝐟𝐠)𝐡 = 𝐟(𝐠𝐡)；
有唯一单位元素 e，使得对∀𝐟 ∈ 𝐆，有𝐞𝐟 = 𝐟𝐞 = 𝐟；
对 $\forall 𝐟 \in 𝐆$ ，存在且唯一存在 $𝐟^{−𝟏}$ 属于 G，使 $𝐟^{−𝟏}𝐟 = 𝐟𝐟^{−𝟏} = 𝐞$ ；这时我们称 $𝐆$ 是一个群，其中元素是群元， $𝐞$ 为其单位元素， $𝐟^{−𝟏}$ 为 $𝐟$ 的逆

例1.1. 一个集合有两个操作E和I， E作用三维欧式空间中任一向量r⃗上，得到r⃗本身， I作用这个r⃗上，得到−r⃗。问{E， I}是否形成一个群？

{E， I}形成一个群，称为空间反演群

例2. 这样一系列操作的集合，它们中每一个操作，都把 1、 2、 ……、 n 这 n 个数，一对一的对应到 1、 2、 ……、 n 这 n 个数上。比如

$P=\left(\begin{array}{cccc} 1 & 2 & \ldots \ldots & \mathrm{n} \\ \mathrm{m}_{1} & \mathrm{~m}_{2} & \ldots \ldots & \mathrm{m}_{\mathrm{n}} \end{array}\right)$

就是把 1、 2、 ……、 n 对应到m1、 m2、 ……、 mn上，其中m1、 m2、 ……、 m n是 1、 2、 ……、 n 的任意排列

所以这些元素的集合也构成一个群，我们称为 n 阶置换群，它的群元的个

数是 n!。在物理上，处理全同粒子体系的时候，会经常用到这一类群

定义群的乘法为数的加法，则全体整数构成一个群， 0 是其中的单位元素， n 与-n 互逆。同理，全体实数也在这个乘法规则下构成一个群，全体复数也是。但如果我们把乘法定义为数乘，那么它们就不再是群了，因为这种情况下单位元素只能是 1，而 0 是没有逆的

有限群与无限群：群内元素个数称为群的阶，当群阶有限时，称为有限群，当群阶无限时，称为无限群

Abel 群：群的乘法一般不可交换（这个在群的定义里面没有体现，因此在一般的群中也不需要遵守），当群中元素乘法可以任意互换时，这个群称为 Abel 群。（由这个定义我们很容易想象 Abel 群的乘法表都应该是相对于对角线对称的）

定理 1.1 重排定理：设𝐆 = {⋯， 𝐠𝛂， ⋯}，对∀𝐮 ∈ 𝐆，当𝐠𝛂取遍𝐆中所有元素时， 𝐮𝐠𝛂给出且仅仅一次给出𝐆中所有元素

两个方面，1) 任何 $G$ 中元素都可以由 $ug_α$ 给出，

2) 仅仅一次给出。

给出。对任意 $g_\beta$ 属于 $G$ ，可取 $u^{−1}g_\beta \in G$ ，使得： $u(u^{−1}g_\beta) \in G$
仅仅一次给出。反证：设有 $g\alpha \neq g\alpha'$ ，使得 $ug\alpha = ug\alpha'$ ，那么就会有： $u^{−1}ug\alpha = u^{−1}ug\alpha′$ ，进而 $g\alpha = g\alpha'$ ，假设矛盾

这都是群本身的性质，不牵扯其内部结构。既然要理解群这个元素集合的结构特性，对其内部结构的认识不可避免。下面的内容很自然与内部结构有关，子群与陪集

# 子群、陪集、正规子群与商群

定义 1.4 子群：设 H 是群 G 的一个子集（部分元素的集合），若对群 G 相同的乘法运算， H 也构成一个群，则称 H 为 G 的子群

显然{e}与 G 本身都是 G 的子群，由于太明显，所以称为显然子群，或平庸子群。而群 G 的非平庸子群称为固有子群。一般我们找群 G 的子群的时候找的是它的固有子群（非平庸子群）。

例5. n 阶循环群，它的定义是 $a^n = e$ ，由 $\left\{a, a^{2}, \cdots, a^{n-1}, a^{n}=e\right\}$ 组成。这样的群是 Abel 群，乘法可易。以 6 阶循环群为例， $G = \left\{a, a^{2}, \cdots, a^{n-1}, a^{n}=e\right\}$ ，其中 ${e}$ 与 $G$ 是显然子群。 ${a^2、 a^4、 e}$ 与 ${a^3、 e}$ 为固有子群。

定义 1.5 群元的阶：对任意一个有限群 $G$ ，从中取一个元素 $𝐚$ ，从 $𝐚$ 出发作幂操作，总是可以构成 $𝐆$ 的一个循环子群 $𝐙_𝐤$ 的，这个 $𝐙_𝐤$ 等于 $\begin{cases}\left.\mathbf{a}, \mathbf{a}^{\mathbf{2}}, \cdots, \mathbf{a}^{\mathbf{k}-\mathbf{1}}, \mathbf{a}^{\mathbf{k}}=\mathbf{e}\right\}\end{cases}$ ，这时称 $𝐤$ （满足这个性质的最小的 $𝐤$ ）为群元 $𝐚$ 的阶。

凭什么说“从a出发，总能构成G的一个循环子群的”？这是因为如果a = e，则Zk等于{e}，问题解决。如果， a ≠ e，则a2 ≠ a（不然a = e），这时，如果a2 = e，则问题又解决了。如 a2 ≠ e，则它必为e与a之外的另一个元素，我把a2、 a放到我的子集中，继续做a3，同样a3 ≠ a2（不然a = e）、也不等于a（不然a2 = e），如果a3 = e，问题解决，如 a3 ≠ e，再把a3放到那个子集中。依次类推，因为G是有限群（阶为n），所以必然存在一个k小于等于n，使得ak = e，来结束这个过程。这时， {a、 a2、 ⋯ 、 ak−1、 ak = e}这个集合自然就形成了k阶循环子群了

定义 1.6 陪集：设𝐇是群𝐆的子群， 𝐇 = {𝐡𝛂}，由固定的𝐠 ∈ 𝐆，可生成子群𝐇的左陪集： 𝐠𝐇 = {𝐠𝐡𝛂|𝐡𝛂 ∈ 𝐇}，也可生成子群𝐇的右陪集： 𝐇𝐠 = {𝐡𝛂𝐠|𝐡𝛂 ∈ 𝐇}。

一是当H是有限子群时，陪集元素个数等于H的阶。因为不可能存在hα ≠ hα′但ghα = ghα′或hαg = hα′g的情况。也就是说子群中元素与陪集中元素一一对应。二是根据这个定义，陪集可以为子群本身。如果上面取的g ∈ H，就是

定理 1.2 陪集定理：设群𝐇是群𝐆的子群，则𝐇的两个左（或右）陪集或者完全相同，或者没有任何公共元素

线性子空间是线性代数的核心概念，也称向量子空间 $V$ ，它具有三个属性：

$V$ 包含 0 向量
加法封闭：如果向量 $u$ 和 $v$ 都在子空间中，则 $u+v$ 也在子空间中；
乘法封闭：如果 $v$ 在子空间中，则它与任何标量 $c\in R$ 数乘的结果 $cv$ 仍在子空间中。

子群 (Subgroup) 之于群，类似于子空间之于包含它的线性空间。

子群以字母 $H$ 表示，因为字母表中， $H$ 是 $G$ 的下一个字母。

$H$ 是 $G$ 的子群，它是包含于 $G$ 中小一点的群，记为 $H\leq G$ ，若 $H\ne G$ ，称 $H$ 为 $G$ 的真子群 (Proper Subgroup)，以 $H\lt G$ 表示。

任何群的平凡子群是指仅由恒等元构成的子群 $\left\{ e \right\}$ 。

$G$ 天生有两个子群：平凡子群 $\left\{ e \right\}$ 和 $G$ 自身，就好像任一个整数都能被 $1$ 和它自身整除那样乏味。我们感兴趣通常是除了这两个子群的其他子群。如果某个群除了这两个无聊的子群外没有其他子群，该群被称为单群 (Simple Group)，它们适合作为构建其他群的组分，其作用类似质数。

欧拉的学生拉格朗日发现，如果 $H\leq G$ ，则 $G$ 的阶数 $|G|$ ( $G$ 中元素的数量）一定可以被 $H$ 的阶数 $|H|$ 整除， $|H|$ 不可能是其他值，这意味着： $H\leq G\Rightarrow |H| \space divides \space |G|$ ，这就是拉格朗日定理 (Lagrange’s Theorem)。

拉格朗日定理很强大，在确定子群时，它能帮助我们大幅减少可能的子群数量，例如：若 $|G|=35$ ，拉格朗日定理告诉我们： $|H|=1,5,7,35$ ，除了这 4 个值外， $|H|$ 不可能是其他值。其中： $|G|=35$ , $|\left\{ e \right\}|=1$ 。

拉格朗日定理的证明可用下图来大致表示： $H$ 是 $G$ 的子群（左图），右图中，在 $G$ 中选一个不属于 $H$ 的元素 $g$ ，将其乘以 $H$ 得到 $gH$ ，注意若非阿贝尔群， $gH$ 和 $Hg$ 是不同的，称 $gH$ 为左陪集 (Left Coset)，可以证明 $H$ 和 $gH$ 无交集不重叠；类似的，在 $G$ 中选择一个不属于 $H$ 和 $gH$ 的元素 $g'$ 乘以 $H$ 得到 $g'H$ ，与前两者都不重叠，…… ，这样一直进行下去，通过选择大小相同但不重叠的陪集，完成对 $G$ 的划分 ( $G$ 是有限群)。

注意：陪集不是子群，因为它没有恒等元 $e$ ，而 $H$ 有。

例 1: 所有整数 $\mathbb Z$ 在 $+$ 下构成群，这个群可以有无数个子群： $\mathbb Z,2\mathbb Z,3\mathbb Z, 4\mathbb Z,5\mathbb Z,\cdots$ 。重点考察下 $5\mathbb Z$ 的情况， $5\mathbb Z$ 将整数 $\mathbb Z$ 分割为 1 个子群和 4 个陪集。注意 4 个陪集不是子群，因为没有恒等元。这 5 个陪集（子群也可视为陪集 $0+5\mathbb Z$ ) 组成了一个新的群，称为商群 (Quotient Group)，记为 $\mathbb Z / 5\mathbb Z$ ， $5\mathbb Z$ 被称为正规子群 $\mathbb N$ (Normal Subgroup)。这些陪集可被视为新的群 (陪集群 Coset Group) 中的元素，比如第 1 个陪集中的任何整数与第 3 个陪集中任何整数相加的结果一定在第 4 个陪集中，可表示为 $\bar{1}+\bar{3}=\bar{4}$ 。

请注意：

商群 $\mathbb Z / 5\mathbb Z$ 不是群 $\mathbb Z$ 的子群，它是一个完全不同的群。
陪集并不总能形成一个群。陪集能组成群的充要条件是对于任何 $y\in G$ ，都能满足 $y^{-1}Ny=N$ ， $N$ 是正规子群，记为 $N\trianglelefteq G$ 。（推导在文末）
陪集群称为因子群 (Factor Group)，记为 $G/N$ ，在该群中，恒等元为 $N$ 。

正规子群和商群是抽象代数中最有用的概念之一，同态、组合序列和** Field Extension **都应用到它。

要找到 $N$ 必须满足的必要条件，使得陪集组成一个子群。

Solution:

对于非阿贝尔群，操作顺序相关，考虑左陪集 $gN$ 的情况；

选取 2 个左陪集 $xN$ 和 $yN$ ；

因为 $N$ 是个子群，其中必然含有恒等元 $e$ ；

$e\cdot x=x\in xN$ ， $y\cdot e=y\in yN$ ；

要 Coset 能组成群，要求： $x\cdot y\in(xN)(yN)$

即： $(xN)(yN) = xyN$

从陪集 $xN$ 中选一个元素 $x\cdot n_1$ , 从陪集 $yN$ 中选一个元素 $y\cdot n_2$

若两者相乘 $(x\cdot n_1)\cdot (y\cdot n_2)\in xyN$

意味着 $(x\cdot n_1)\cdot (y\cdot n_2)= x\cdot y\cdot n_3$

即： $x^{-1}\cdot(x\cdot n_1)\cdot (y\cdot n_2)= x^{-1}\cdot (x\cdot y\cdot n_3)$

$n_1\cdot y\cdot n_2= y\cdot n_3$

$y^{-1}\cdot n_1\cdot y\cdot n_2= y^{-1}\cdot y\cdot n_3$

$y^{-1}\cdot n_1\cdot y\cdot n_2= n_3$

$y^{-1}\cdot n_1\cdot y\cdot n_2\cdot n_{2}^{-1}= n_3\cdot n_{2}^{-1}$

$y^{-1}\cdot n_1\cdot y= n_3\cdot n_{2}^{-1}\in N$

所以要 $(xN)(yN) = xyN$ ，就需要 $y^{-1}\cdot N\cdot y\in N$ 。

$y^{-1}\cdot N\cdot y\$ 称为共轭。

有兴趣的话也可以尝试反方向的推导，要简单一些。

# 循环群

循环群 (Cyclic Groups)，所有群成员都是群内其他成员的若干次方

定义：若 $G$ 是一个群，群中一个元素 $g\in G$ 能通过 $g^{n}, n\in Z$ 来构成群内所有的元素，则！[公式] (opens new window) 就是一个循环群，元素 $g$ 被称为群的生成器 (generator)，记为： $G=\langle g\rangle$ . 注意在乘法下 $e=1$ ， $n$ 可为负数；若在加法下， $e=0$ ，那么就要通过 $ng, n\in Z$ 来“生成”群元素了。

例 1: 加法下的整数 $\mathbb Z$ 所构成的群的生成器是 1： $\mathbb Z=\langle 1\rangle$ . 其中 $e=0$ ， $1$ 的逆为 $-1$ ，封闭性要求必须包含 1 和-1 所有的倍数，于是 1“生成”了所有的整数。

定理 1：每个循环群都是阿贝尔群。

# 同构

所谓同构 (isomorphism)，字面上粗略的理解就是两个结构相同的群，这个理解大方向是对，但对“结构”、“相同”的定义还不够明确。非正式的，可认为群同构是指群 $G$ 和群 $H$ 的结构和大小 (size) 相同，且两个群的元素间满足双射 (Bijection=Injection+Surgection)。

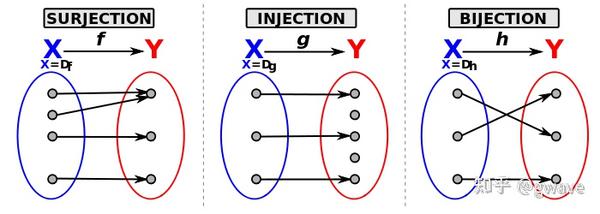
同构的两个群有点像：你在 4S 店中买车，面对两辆几乎完全一样的车。

仅仅满足双射是不够的，元素还必须整合在一起以相同的方式工作。若只满足双射，有可能出现以下场景：两辆车的零部件相同，一辆车已装配完毕，随时可以开走，而另一辆车则还处于一堆零件状态。

同构是相同类型的两个群之间的能保持结构的映射 (structure-preserving mapping)，可通过逆映射 (inverse mapping) 反转 (reverse)。

因此，同构需要满足的条件：假设群 $(G,\circ)$ 和群 $(H,\cdot)$ 之间存在双射 $f:G\rightarrow H$ ，使得 $f(a)=A$ 和 $f(b)=B$ ，如果这两个群是同构的，那么 $a\circ b$ 应对应 $A\cdot B$ ，即 $f(a\circ b)=A\cdot B=f(a)\cdot f(b)$ . 该条件必须对 $G$ 中所有的元素 $a$ 和 $b$ 都成立。

若 $G$ 与 $H$ 同构，记为： $G\cong H$ 。

TODO: (1 封私信 / 81 条消息）如何（直观地）的理解同态和同构？ - 知乎 (zhihu.com) (opens new window)

# 同态

群论中最重要的概念——群同态 (group homomorphism) 了，它被广泛应用于数学和物理等领域。

如果有两个群—— $G$ 和 $H$ ，如何对两者进行比较？使用什么特征来比较？如何测量两者间是多么相似或不同？“相似”是怎么定义的？

需要引入同态 (homomorphism) 的概念。

先把名字掰扯清楚。Homomorphism 这个词来自古希腊语：ὁμός(homos) 意为“同样的，一样的” (Same)，μορφή(morphe) 意为“形式”或“形状”(Shape)。

1892 年，德国数学家克莱因 (Felix Klein, 1849–1925) 引入了 Homomorphism 一词，本来他想表达的意思是“相似 (Similar) 的形式”，但由于德语ähnlich（“相似”）与希腊语ὁμός（“同样”）的错误翻译，英文的意思变成了“相同的形式”，中文译为同态。同态 (Homomorphism) 这个词原本希望表达的含义是“似态”，但以讹传讹，变成了同态。

真正“相同的形式”的以 Isomorphism 表达，中文译为“同构”（参见上一篇文章 (opens new window))。

上篇文章提到，同构是满足双射的同态，也就是说，同态本身并无双射的要求。

定义：给定两个群 $(G, ∗)$ 和 $(H, ·)$ ，从 $(G, ∗)$ 到 $(H, ·)$ 的群同态是：函数 $f: G → H$ 使得对于 $G$ 中的所有 $u$ 和 $v$ 成立： $f(u*v)=f(u)\cdot f(v)$ 。

分析：

$f: G → H$

$u*v=w$

$u\mapsto f(u),v\mapsto f(v),w\mapsto f(w)$

同态的目的是保持形式不变： $u*v=w\Rightarrow f(u)\cdot f(v)=f(w)$

将 $w=u*v$ 带入右侧 RHS： $f(u)\cdot f(v)=f(u*v)$

这就是同态的定义，看上去很简单的样子。

例 3: $G=(\mathbb R,+)$ , $H=(\mathbb R^{+},\times)$

$G$ 是阿贝尔群， $e=0$ ； $H$ 是阿贝尔群， $e=1$

$f: G → H$ $x \mapsto e^{x}$

$f(x+y)=e^{x+y}=e^x\times e^{y}=f(x)\times f(y)$

故 $G，H$ 同态。

例 4: $G=(\mathbb C^{\times},\times)$ , $H=(\mathbb S^{1},\times)$ with $|z|=1$

$\mathbb C^{\times}$ 是指非 0 复数； $\mathbb S^{1}$ 的 S 表示球面 Sphere，1 表示维度，1 维的球面是个圆。这两个符号均为标准符号。

$f: \mathbb C^{\times}\rightarrow\mathbb S^{1}$

$f(re^{i\theta})=e^{i\theta}$

该映射将任意模长的复数都 Scale 到单位元上，因此，肯定不是 1:1，这也是同态，但显然不是同构。证明步骤不复杂，可以自行推导。

# 拓扑的同态

如何“数学的”判断两个拓扑是否同态？欧拉示性数公式： $\chi=V-E+F$ ，V、E 和 F 分别代表顶点、边和面的数量。比如立方体的顶点、边和面的数量分别是 8、12 和 6，它的欧拉示性数等于 2。球与正方体同态，所以球的欧拉示性数也是 2，其实任何凸多面体的欧拉示性数都是 2。

当且仅当两个面的欧拉示性数相等时，这两个面同态。

如何计算（没有顶点和面）的甜甜圈的欧拉示性数？两个方法：1）三角化 (triangulation)，计算其同态的欧拉示性数。

\2) 使用公式： $\chi = 2- 2g$ ， $g$ 为亏格 (genus)，可简单理解为孔的数量。篮球没有孔， $g=0$ ；甜甜圈有一个孔 $g=1$ ; 分别对应的 $\chi$ 为 2 和 0。

显然，2 个和 3 个孔的甜甜圈的 $\chi$ 分别为-2 和-4.

同构是同态的一种，是双射的同态。

两个群同态，不是说它们是完全相同，只能说它们具有相似之处。

下一篇文章将介绍同态核 Kernel，对应线性代数中的零空间。

# Kernel / Image 与零空间/列空间

同态的映射不一定是 1:1（单射，Injection) 的，那能否衡量该映射与单射相差多少呢？于是需要引入核 (Kernel) 的概念。

还记不记得，线性代数中的零空间也被称为核呢？

# 1. 代数中 Image 与 kernel

先复习下 Image 和 Kernel 的通用概念。

$f$ 是从域 (Domain) X 到陪域 (Codomain) Y 的函数。 Y 内的黄色椭圆 $f(x)$ 是 $f$ 的像 (Image)。函数的像是该函数可能产生的所有输出值的集合。线性代数中， $Ax=b$ ，若将矩阵乘法视为函数 $f(x)=Ax$ ，则 $b$ 所在的列空间被称为 image 是很合理的

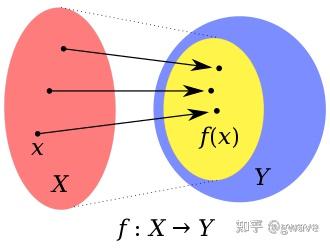
抽象代数中，同态的核是恒等元 1（下图中 1 代表恒等元，并非实际的数值 1) 的逆像 (Inverse Image)。下图中，映射 $h$ 将左侧 $G$ 中绛红色圆圈 kerh，映射到右侧 $H$ 中的一个点 1（恒等元）； $H$ 中的颜色与 $G$ 相同的椭圆是 $h$ 的 image。请注意，恒等元 1 也位于左侧的 kerh 中。

下面会讨论到，对于矩阵乘法来说，kernel 对应零空间。

之前讲过正规子群 $N$ 包含恒等元，其实 Kernel 就是 $G$ 的正规子群 $N$ ， $aN$ 是陪集 (coset)。

TODO: 什么是正规子群

定义：映射 $h$ 的核是 G 中映射到 H 恒等元的元素集合。 $\ker(h)\equiv\{x\in G : h(x)=e_H \}=h^{-1}(e_H )$ ; $h$ 的像 (image): $Im(h)\equiv h(G)=\{h(x):x \in G\}$ .

# 2. 核的推导与属性

假设 $G$ 和 $H$ 同态， $f$ 非 1:1 映射，也就是说， $G$ 中至少有两个元素会映射到 $H$ 中的同一个元素，假设： $x_1,x_2,\cdots$ 都映射到 $y$ ，即 $f(x_1)=y,f(x_2)=y,\cdots$ 。

同态有两个特性（证明在文末）：

恒等元映射到恒等元
逆映射到逆

所以上式两边可同乘以逆 $f(x_1^{-1})$ ： $f(x_1)f(x_1^{-1})=yf(x_1^{-1});f(x_2)f(x_1^{-1})=yf(x_1^{-1}),\cdots$

根据同态的定义： $f(x_1x_1^{-1})=yy^{-1};f(x_2x_1^{-1})=yy^{-1},\cdots$

$f(x_1x_1^{-1})=e_H;f(x_2x_1^{-1})=e_H,\cdots$

显然 $G$ 中存在多个元素 $x_1x_1^{-1},x_2x_1^{-1},\cdots$ 映射到 $e_H$ ，这些元素的集合就是核，记为： $\ker(h)=\{ x \in G:f(x)=e_H\}$ ，注意： $\ker(h)$ 的表达强调了核是同态的属性，而不是群的属性。

上面推理表明，如果不是 1:1，那么 $\ker(f)$ 中的元素数量必然大于 1，因此，可使用 Kernel 来衡量映射与 1:1 的差距。

$f(e_G)=e_H\Rightarrow e_G \in \ker(f)$ ，说明 Kernel 肯定不会是空集，至少有一个元素 $e_G$ 。

反之，如果 kernel 只包含恒等元一个元素，则说明映射是 1:1。

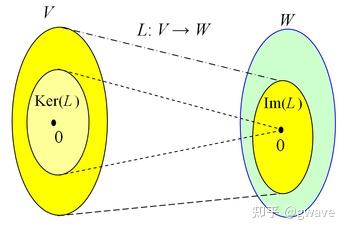
# 3. 同构第一定理

同构定理 (The Isomorphism Theorem for Groups) 也称 Noether 同态定理，共 3 个，由 Emmy Noether 在 1927 年提出，这里讨论第一定理。Emmy Noether 的工作影响深远，可参考下文文末的介绍，某种程度上，这是写这个系列的原因，希望能打通代数、几何/拓扑和分析。gwave：导数，可能和你了解的不同（上） 25 赞同 · 5 评论文章 (zhihu.com) (opens new window)

若 $f: G\rightarrow H$ 同态，则 $Im(f)\cong \frac{G}{ker(f)}$ .

对应到矩阵子空间， $Im(L)$ 是列空间， ${\ker(L)}$ 是零空间，即 $Im(L)\cong \frac{V}{\ker(L)}$ 。如果维度是有限的，则： $\dim(Im(L))+\dim(Ker(L))=\dim(V)$ ，即 Rank–nullity 定理。

# 4. 同态属性证明两则

证明 1: 同态群恒等元映射到恒等元。

选择非恒等元的任意元素 $x \in G$ ，

$x*e_G=x$

$f(x*e_G)=f(x)$

$f(x)\cdot f(e_G)=f(x)$

$f(x)$ 是 $H$ 中的一个元素，假设 $f(x)=y$

$y\cdot f(e_G)=y$

$y^{-1}y\cdot f(e_G)=y^{-1}y$

$f(e_G)=e_H$

证明 2: 同态群逆元映射到逆元。

假设： $f(x)=y,x \in G, y\in H$

$x*x^{-1}=e_G$

$f(x*x^{-1})=f(e_G)$

$f(x)\cdot f(x^{-1})=e_H$

$y\cdot f(x^{-1})=e_H$

$y^{-1}y\cdot f(x^{-1})=y^{-1}e_H$

$f(x^{-1})=y^{-1}$

# 对称群

凯莱定理 (Cayley's theorem) 说：排列——这种工具足够强大，可用来建立任意群。

$n$ 个对象所有的重新排列组成对称群 $S_n$ ， $S$ 表示对称 Symmetric.

虽然对 $n$ 个对象进行排列构成一个群，但是建立一个排列群并非一定需要所有的排列，通常 $S_n$ 的子集就可以构成群，一种著名的方法就是取一半 $S_n$ 的元素，构成交错群 $A_n$ ，但是并非随意选一半都能构成群，但如果选取 $S_n$ 中每个元素并对其进行平方，平方后得到的元素整好是 $S_n$ 的一半，称为交错群 (Alternating Group) $A_n$ 。

诺特定理的基本内容是 “any differentiable symmetry of the action of a physical system has a corresponding conservation law”，也可以说是任何一个保持拉格朗日量不变的微分算符，都对应一个守恒的物理量。

jokervTv 爬坑历程

Choose mode

群论入门

群论入门

# 模算术

# 群的定义

# 子群、陪集、正规子群与商群

# 循环群

# 同构

# 同态

# 拓扑的同态

# Kernel / Image 与零空间/列空间

# 1. 代数中 Image 与 kernel

# 2. 核的推导与属性

# 3. 同构第一定理

# 4. 同态属性证明两则

# 对称群